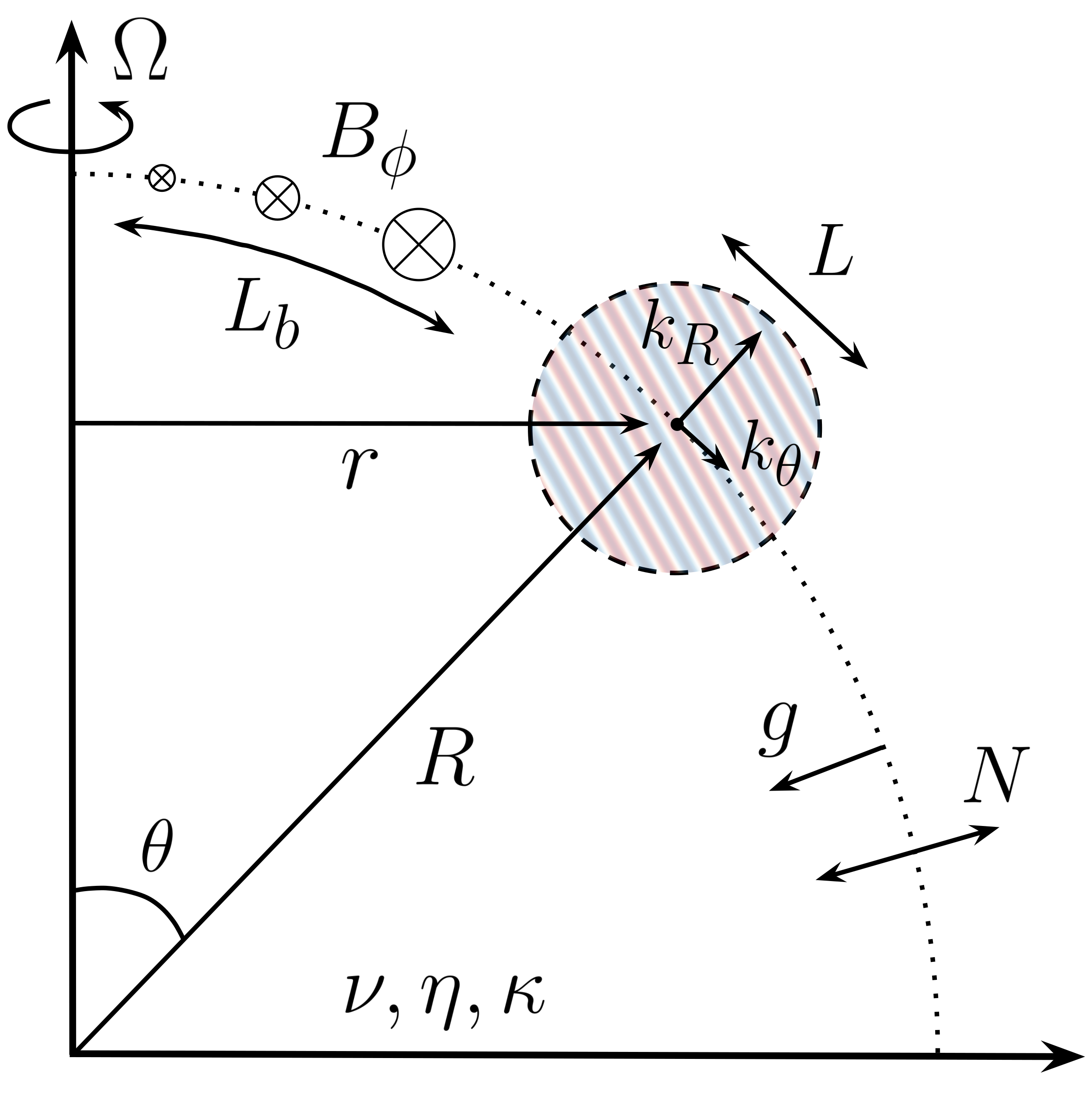
Tayler instability of toroidal magnetic fields Bϕ is broadly invoked as a trigger for turbulence and angular momentum transport in stars. This paper presents a systematic revision of the linear stability analysis for a rotating, magnetized, and stably stratified star. For plausible configurations of Bϕ, instability requires diffusive processes: viscosity, magnetic diffusivity, or thermal/compositional diffusion. Our results reveal a new physical picture, demonstrating how different diffusive effects independently trigger instability of two types of waves in the rotating star: magnetostrophic waves and inertial waves. It develops via overstability of the waves, whose growth rate sharply peaks at some characteristic wavenumbers. We determine instability conditions for each wave branch and find the characteristic wavenumbers. The results are qualitatively different for stars with magnetic Prandtl number Pm ≪ 1 (e.g., the Sun) and Pm ≫ 1 (e.g., protoneutron stars). The parameter dependence of unstable modes suggests a nonuniversal scaling of the possible Tayler–Spruit dynamo.
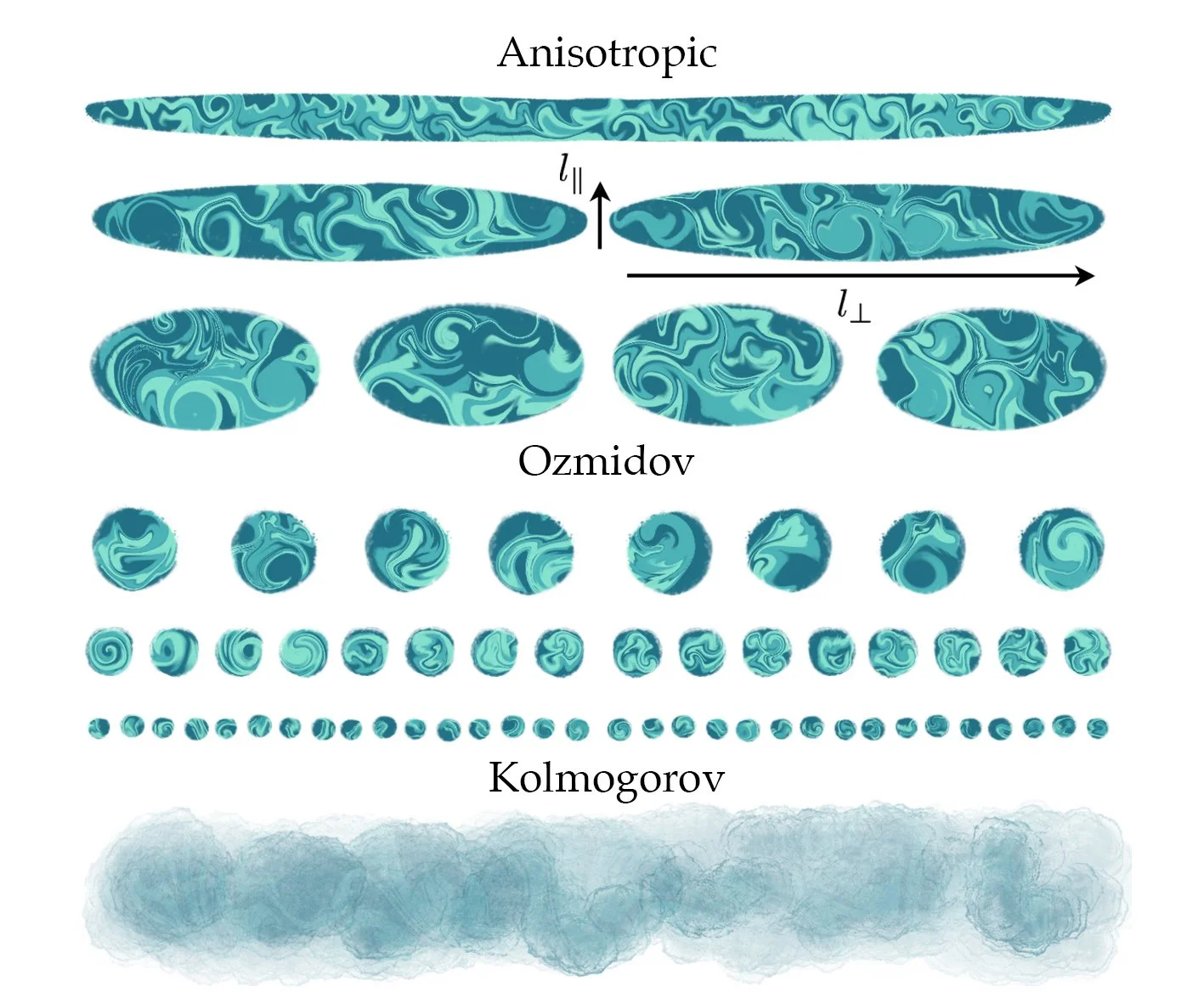
We extend the scaling relations of strongly (stably) stratified turbulence from the geophysical regime of unity Prandtl number to the astrophysical regime of extremely small Prandtl number applicable to stably stratified regions of stars and gas giants. A transition to a new turbulent regime is found to occur when the Prandtl number drops below the inverse of the buoyancy Reynolds number, i.e. PrRb<1, which signals a shift of the dominant balance in the buoyancy equation. Application of critical balance arguments then derives new predictions for the anisotropic energy spectrum and dominant balance of the Boussinesq equations in the PrRb≪1 regime. We find that all the standard scaling relations from the unity Pr limit of strongly stratified turbulence simply carry over if the Froude number, Fr, is replaced by a modified Froude number. The geophysical and astrophysical regimes are thus smoothly connected across the PrRb=1 transition. Applications to vertical transport in stellar radiative zones and modification to the instability criterion for the small-scale dynamo are discussed.
We derive scaling relations based on freefall and isotropy assumptions for the kinematic small-scale dynamo growth rate and amplification factor over the course of the mixing, saturation, and decay phases of the Rayleigh–Taylor instability (RTI) in a fully ionized plasma. The scaling relations are tested using sets of three-dimensional, visco-resistive MHD simulations of the RTI. They are found to hold in the saturation phase, but exhibit discrepancies during the mixing and decay phases, suggesting a need to relax either the freefall or isotropy assumptions. Application of the scaling relations allows for quantitative prediction of the net amplification of magnetic energy in the kinematic dynamo phase and therefore a determination of whether the magnetic energy either remains sub-equipartition at all velocity scales or reaches equipartition with at least some scales of the turbulent kinetic energy in laboratory and astrophysical scenarios. As an example, we consider the dynamo in RTI-unstable regions of the outer envelope of a binary neutron star merger, and predict that the kinematic regime of the small-scale dynamo ends on the timescale of nanoseconds and then reaches saturation on a timescale of microseconds, which are both fast compared to the millisecond relaxation time of the post-merger.
We present numerical investigations into three principal properties of a small-scale dynamo in stably stratified turbulence: the onset criterion, the growth rate, and the nature of the magnetic field anisotropy in the kinematic regime. The results suggest that all three dynamo properties are controlled by the scale separation between the Ozmidov scale and the viscous or resistive scale. In addition to the critical magnetic Reynolds number, this allows for the definition of critical buoyancy and magnetic buoyancy Reynolds numbers for stratified small-scale dynamo onset in the high and low magnetic Prandtl number regimes, respectively. The presence of a small-scale dynamo in stellar radiative zones could affect dynamics through the resulting Maxwell stresses or its influence on large-scale dynamo mechanisms in regions of differential rotation. Taking the solar radiative zone as a representative example and applying the onset criterion, we find that the stratification is strong enough to make the small-scale dynamo marginally active in the stably stratified turbulence of the solar tachocline.